两轮自平衡小车的数学建模

作者：Rick Grimes

模型假设与符号说明

平衡车在运行过程中，在不考虑转向的情况下，基本上是沿着一个固定的轴做直线运动，所以，平衡车的运动可以理解为在竖直二维平面上的一种运动，该运动形式的基本组成包含了车体前后移动与车体本身绕着电机轴径的转动两种运行状态，并且这两种运行状态之前有着紧密的耦合关系。因此，对于若要从数学模型的角度定量的分析平衡车的动力学原理，则需要对根据平衡车的基本运动特点对所研究的问题进行合理的假设与简化。

模型假设一 不考虑平衡车的转向，其运动为沿着y轴在y-o-z平面上的运动，其转动轴沿着x轴。如图1所示。

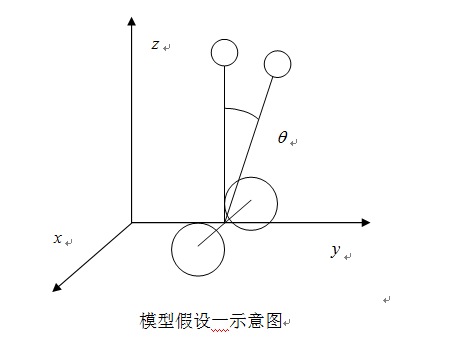
图1 模型假设一示意图

模型假设二 由于倒立摆系统是非惯性系的运动系统，其本身就具有不稳定特性，因此，在分析平衡车的数学模型时，为了简化计算，假设其所受到的外部干扰作用方向垂直于车体的转动半径。

模型假设三 平衡车的初始状态，其轮子的加速度为0。车体倾角为0。

符号说明 模型分析与建立时用到的相关符号说明，见下表。

表1 符号说明

基于倒立摆系统的平衡车受力分析

在前文的介绍中可知，自平衡车的受力形式与力学中的倒立摆系统是类似的，因此，结合倒立摆的相关知识，在对平衡车进行建模之前，首先从静态的受力分析角度对其进行分析。

对于常规的单摆运动来说，最终都能在竖直方向上的稳定。造成单摆最终能够自主稳定的原因就是单摆运动时所受到的回复力与单摆的位移在任意时刻都是相反的，这就导致了单摆无法在产生摆动角度的时候保持稳定状态。如图2所示。那么，从运动位移与回复力的关系入手，把单摆倒置形成倒立摆，质心的受力情况则变成了图3所示的情况。

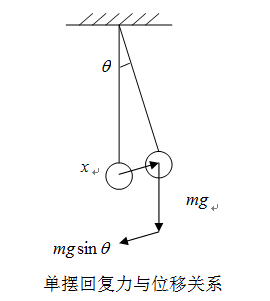
图2 单摆回复力与位移关系

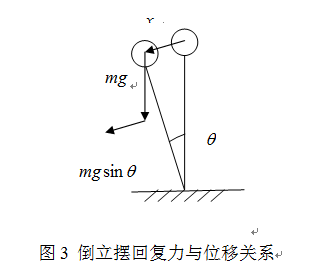
图3 倒立摆回复力与位移关系

由图3的受力分析可以看出，倒立摆的回复力与位移始终保持同方向，因此，倒立摆系统无法实现自主的稳定。在此基础上继续深入分析可知，如果想让倒立摆保持稳定，在重力无法改变的前提下，我们只需要加入一个力，使其受到的合力符合单摆模型的受力特点，即可使倒立摆实现稳定。

结合平衡车的自身结构可知，平衡车相对于倒立摆不同的地方在于，平衡车的底端是可移动的轮轴。因此，让平衡车的轮子产生某一方向的加速度，选取车身轮轴的连接点为研究对象，使平衡车构成一个非惯性系，那么对于车体本身来说，即受到一个非惯性力的作用，这个力的方向与倒立摆的回复力的方向相反。在此基础上再次对平衡车进行受力分析，加入车轮加速度 之后的受力情况如图4所示。

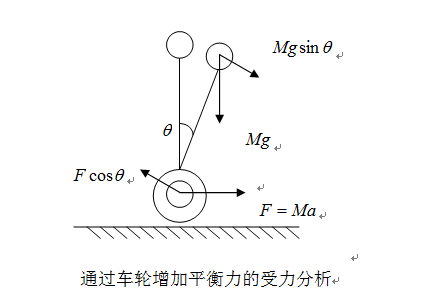
图4 通过车轮增加平衡力的受力分析

此时，倒立摆所受到的回复力为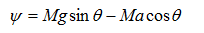： （2-1）

对（2-1）进一步分析，我们可以假设在小角度范围内，电机提供的力 正比于车体倾角 ，其比例系数为 。由此线性关系，结合工程学的小角近似，可以得到关于回复力加速度 与电机提供的加速度的比例系数 之间的关系：

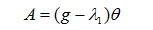（2-2）

分析（2-2）的式子，可以很轻易的知道，要想让平衡车稳定，电机需要提供一个加速度，并且其加速度与车身倾斜角度的比值必须大于重力加速度 。这样，车身回复力的方向便可以与其产生的位移反向，形成单摆的受力形式。即实现了倒立摆运动到单摆运动的转化。

通过上述分析，从理论上已经确定了控制车体平衡的相关变量。但是实际运行中，单摆恢复平衡状态过程中还会受到阻尼力的作用，使系统的稳定时间较短。打到稳定的速度更快。实际运行时，阻尼力可以来自于空气阻力，摩擦阻力等等。但是对于自平衡车这种倒立摆系统，这些自然存在的阻尼力还不足以实现让其快速稳定的效果，因此，在无阻尼的平衡过程中， 车体将会产生大幅度的摆动现象。为了消除这一现象，在（2-1）的基础上，人为增加阻尼力来提高稳定的快速性。增加阻尼力之后的受力情况如图5。

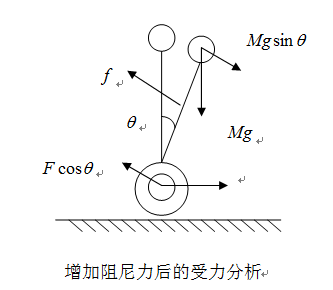
图5 增加阻尼力后的受力分析

通过受力分析可得，此时回复力为：

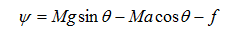（2-3）

同样的，为了突出主要影响因素，忽略次要因素，简化分析过程，从而假设阻尼力与其角速度的关系成正比，即：

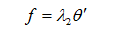（2-4）

至此，可得车体回复力所产生的加速度的完整表达式：

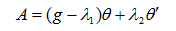（2-5）

分析（2-5）可以知道，若要想让平衡车保持自稳定，需要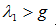 ，同时 。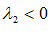

以上我们通过把倒立摆受力模型转化到单摆受力模型这一过程，详细的分析了其中受力的过程，并且得到了平衡车的控制参数。下面，我们根据上面的简单受力分析，对平衡车运动过程运用微分方程来建立一个完整的动态数学模型，并且结合经典控制理论的分析方法更深一步的探讨平衡车的控制方法。

自平衡车数学模型建立

考虑到小车倾斜时，是一个在小范围内动态的转动过程，因此，用物理学中的刚体旋转的相关物理量去描述平衡车的动态过程。

通过上文的分析，可以知道倒立摆系统的回复力产生的回复加速度应为重力沿着车体旋转路径的切向分量叠加上车轮加速产生的非惯性力，并且再叠加上系统的阻尼力。因此，仍然从这一受力关系上入手，建立总的切向加速度与各个分量加速度之间的关系。

引理 切向加速度等于角加速度乘以曲率半径。

设车轮产生的加速度为 ，方向沿着水平方向。外部对车体的干扰产生的加速度为 ，方向为时刻垂直于车体，车体倾斜的角度随着时间的变化关系为 ，并且已知车体的旋转半径（车体轮轴到顶端的高度） 。因此可以建立平衡车运动时的动态数学模型如下：

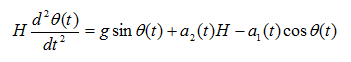（2-6）

进一步分析（2-6）可知在车体初始状态下，车轮的加速度应为0， 的产生应该由角度的变化引起，因此以模型的初始状态为研究对象，可以略去包含 的项。（2-6）可以化简为如下形式：

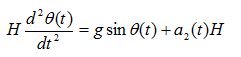（2-6）

同时，为了突出角度与时间的线性关系，对（2-6）进一步用小角近似进行简化，最终可以得到平衡车的微分方程模型：

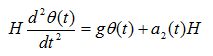（2-6）

以上，通过建立微分方程，得到了自平衡车在时域上的动态数学模型。下面对（2-6）进行详细分析讨论。

自平衡车数学模型计算与分析

在上文建立的数学模型的基础之上，利用经典控制理论的分析方法，对平衡车的数学模型进行相关的计算与分析，可以很精确的得到平衡车的稳定控制方法。

首先，对（2-6）的微分方程模型进行拉普拉斯变换，得到其在S域对应的传递函数：

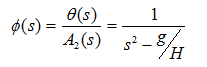（2-7）

由得到的平衡车传递函数，调用Matlab软件，绘制出 的根轨迹示意图，如图6所示，代码详见附录matlab部分。并调用[p z]=pzmap(num1,den1)命令语句，计算出该传递函数的零极点。

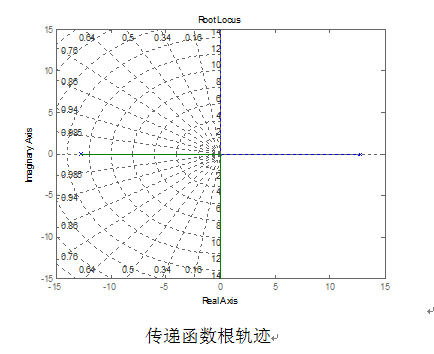
图6 传递函数根轨迹

通过根轨迹的示意图可以很清晰的看出，平衡车的传递函数对应的两个零极点，有一个在S平面的右半平面，这就很好的解释了为什么平衡车是一个不稳定系统。下面，根据自平衡车传递函数，增加相关的环节来对平衡车的传递函数进行校正。

在系统实际运行过程中，仅仅通过调整放大器的增益是不能够满足给定的性能指标的要求的，，这就需要在原系统中加入一些参数可调的装置来改善控制系统的性能，而引入的的附加装置就成为校正装置。经典控制理论中常见的校正方式通常有串联校正、反馈校正、复合校正三种方式。除此之外，工程上常用的还有PID校正器 。

PID校正器由比例P，积分I，微分D这三种基本规律组合而成。常用的有P控制，PD控制，PI控制与PID控制。在文章的第4章中，结合平衡车的程序实现，详细的论述PID控制器的特点与选择。此处只稍作介绍。 考虑到PD控制规律中的微分项能反映输入信号的变化趋势，产生有效的早起修正信号，以增加系统的阻尼程度，从而改善系统的稳定性。因此对于自平衡车系统的校正，在此选取PD控制作为校正方法。同时，考虑到反馈校正方式除了能达到常规串联校正的效果之外，还能消除被反馈校正所包围部分的系统不可变参数的波动对系统控制性能的影响。因此选取反馈形式的PD校正器作为改善自平衡车系统性能的方案。加入反馈PD控制回路之后的系统结构图如下图7所示。

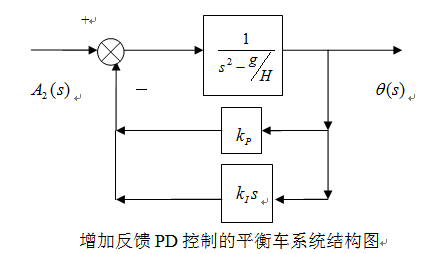
图7 增加反馈PD控制的平衡车系统结构图 在反馈通路中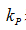，表示比例项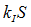，表示微分项，该反馈通道增加后的效果应该是减小车身的倾斜，因此，反馈通路必须是负反馈，才能达到减小车体倾斜的目的。增加负反馈之后，自平衡车系统的传递函数变为：

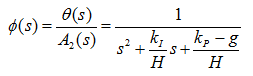（2-8）

通过代数求解可得当前传递函数的极点表达式：

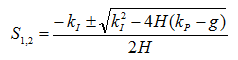（2-9）

通过分析（2-9）可知，若要想让两个极点位于S平面左半平面来保证系统是稳定的，那么就需要满足 ， 。在此结论下，调用Matlab软件绘制当前系统传递函数的根轨迹并且求解极点值。如图9所示。

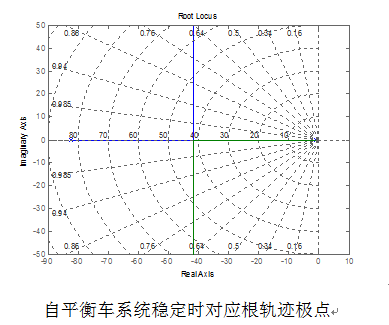
图9 自平衡车系统稳定时对应根轨迹极点

通过图9的展示，可以很清晰的看到，此时系统传递函数的极点都已经分布在了S平面的左半平面，适当的调整参数，极点的位置将会进一步远离0点，系统将会更稳定，在此只做示意分析，不再深入讨论参数的选取。

可见，对于自平衡车系统，采取PD控制，构成闭环负反馈系统，适当调整参数，可以有效的控制其稳定性。在此基础上，数学模型还要求控制系统的硬件部分能够精确的解算车体的实时角度，并且能够提使电机供相应的加速度。这些硬件条件将会在后续章节详细进行论述。

基于simulink的自平衡车数学模型仿真

通过对自平衡车系统进行建模分析，从理论上得到了自平衡车的控制方法。下面，调用Matlab软件的Simulink仿真工具包对自平衡车的控制系统数学模型进行仿真验证，观察角度在干扰信号的作用下的自恢复情况.

在Simulink文件中，建立自平衡车的数学模型，调用PID控制器构成控制系统的主要部分。设定输入信号值为0，代表角度初始值为0，平衡车初始在平衡位置。对输出节点，调用两个Step模块，通过设定Step Time，使之构成宽度为1s的脉冲信号作为平衡车的外力干扰作用信号。整体系统构成负反馈形式。如图10.

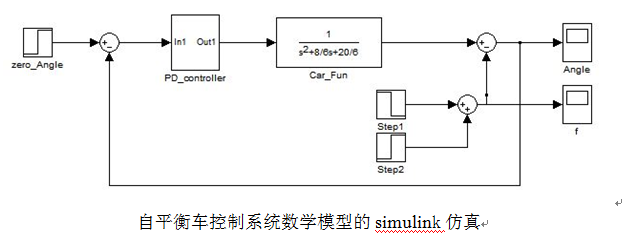
图10 自平衡车控制系统数学模型的simulink仿真

仿真系统中示波器Angle与f分别表示角度变化波形与外力作用信号波形。点击运行之后可以很清晰的看到，外力作用为标准的脉冲信号。如图11。 此时，在脉冲信号作为干扰的情况下，Angle示波器中显示了车体角度的变化值，如图12。通过波形可以看出，角度在外界干扰的情况下，能够在一定时间内自动恢复到稳定状态。证明了前文建立的自平衡车控制系统的数学模型是行之有效的。

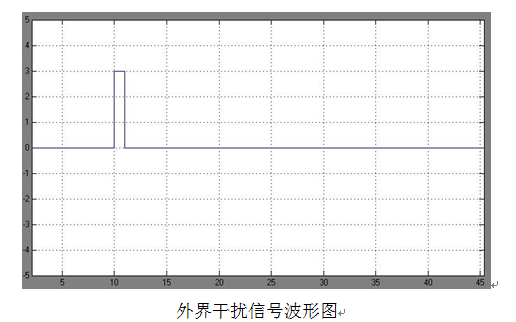
图11 外界干扰信号波形图

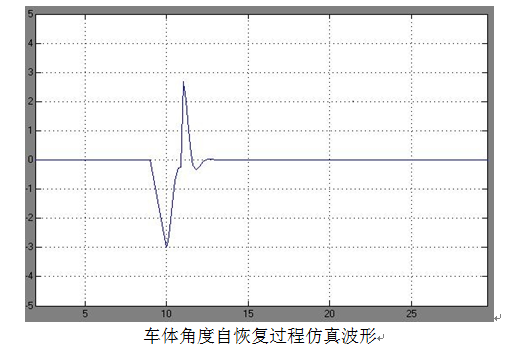
图12 车体角度自恢复过程仿真波形

本章小结

本章基于对平衡车做出的几个基本合理假设，首先从物理学中倒立摆系统入手，结合平衡车的结构特点进行了详细的受力分析，得到了控制平衡车稳定的参数要求。同时，在受力分析的基础上，进一步建立了平衡车在时域上的的微分方程模型，动态的描述了平衡车的运行特征。之后根据经典控制理论，得到平衡车的传递函数，在S域利用matlab软件对平衡车的稳定性做了探讨。得到了系统由于在S平面右半平面有极点而不稳定的结论。之后在此基础上，选取PD控制，在平衡车系统传递函数的基础上增加负反馈通道对系统进行校正。然后利用matlab在此分析了系统的稳定性，得到了稳定的结论。为下一步实际设计小车的软硬件系统提供了理论支持。

附：

本章讲解中用到的Matlab文件：百度云传送门