互补滤波器

作者：Songyimiao

参考：《The Balance Filter》

加速度计在短时间内收到车体震动等因素干扰会产生高频振荡的噪声信号，因此可信度降低。

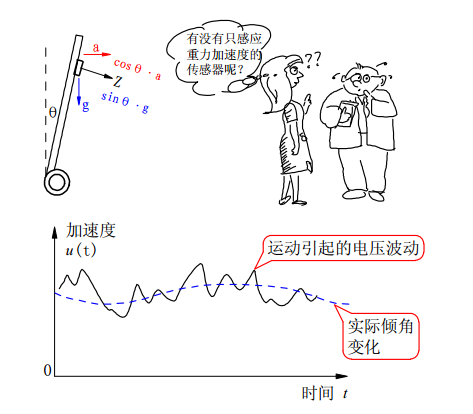
车体运动引起加速度信号波动

而陀螺仪由于是积分计算角度，因此任意时刻的微小误差将会随着时间的推移在积分过程中被放大，导致陀螺仪数据产生漂移，因此长时间内陀螺仪的可信度较低。

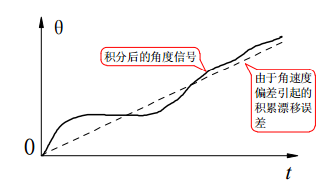
陀螺仪积分误差

针对这种情况，MWbalanced(STC15)滤波算法采取一阶互补滤波算法，对加速度计与陀螺仪的数据进行处理，得到精准的角度。下面，我们对一阶互补滤波算法进行详细的论述。

想要得到精准的姿态数据，必须得经过滤波，去除噪音呀。可是滤波算法千万种，就两轮自平衡小车而言，常见的就有互补滤波、卡尔曼滤波等等。

如果一上来就挽起袖子，豪言壮志要撸卡尔曼滤波，没点基础的初学者可能会一脸懵逼。

那么，我们还是先把最简单有效的互补滤波先捋一遍。

//———————我是华丽丽的分根线———————//

滤波器通常有模拟滤波器和数字滤波器。模拟滤波器完全依靠电阻器、电容器、晶体管等电子元件组成的物理网络实现滤波功能。数字滤波器是由数字乘法器、加法器和延时单元组成的一种算法或装置，功能是对输入离散信号进行运算处理，以达到实现滤波的目的。

我们下面讨论的各种滤波器，都属于数字滤波器。

在了解互补滤波器之前，先来了解三个基本概念。

• 低通滤波器
• 高通滤波器
• 带通滤波器

低通滤波器（英语：Low-pass filter）容许低频信号通过，但减弱（或减少）频率高于截止频率的信号的通过。’低’和’高’频率的含义，是相对于滤波器设计者所选择的截止频率而言的。

高通滤波器则相反，而带通滤波器则是高通滤波器和低通滤波器的组合。

互补滤波器，也是带通滤波器的变种。

（一阶）互补滤波核心代码非常简洁：

angle = (0.98)*(angle + gyro * dt) + (0.02)*(x_acc);

其中，angle为得到的实际角度，gyro为陀螺仪值，x_acc为加速度数据换算后的角度值，dt为计算周期；

积分器

学过高中物理的同学都知道，速度*时间=路程。如果知道了起点位置、速度和时间，通过计算就能得到路程。转化为代码就是：

position += speed*dt;

其中，position为路程，speed为速度，dt为计算周期。speed*dt 得到计算周期时间段内通过的路程，通过对该路程的积分（不断累加），得到系统运行以来的路程。

同理，通过对角速度的积分，即可得到角度。

angle += gyro*dt; 

其中，angle为角度，gyro为陀螺仪角速度，dt为计算周期。gyro*dt 得到计算周期时间段内通过的角度，通过对该角度的积分（不断累加），得到系统运行以来的角度。

互补滤波器中angle = (0.98)*(angle + gyro * dt) + (0.02)*(x_acc)中(angle + gyro * dt)是一个积分器，工作原理和上面说的一样。

低通滤波器

低通滤波器的目标是过滤掉短期波动，让长期变化得以保留。

angle = (0.98)*angle_last + (0.02)*x_acc;

其中，angle为当前角度，angle_last为前一次角度，x_acc为当前加速度计换算后的角度值。对x_acc进行低通滤波，让加速度计的长期变化得以保留，angle能追踪加速度计的长期变化。

（一阶）互补滤波器

互补滤波器，就是上面积分器和低通滤波器的变种结合体。如图1。

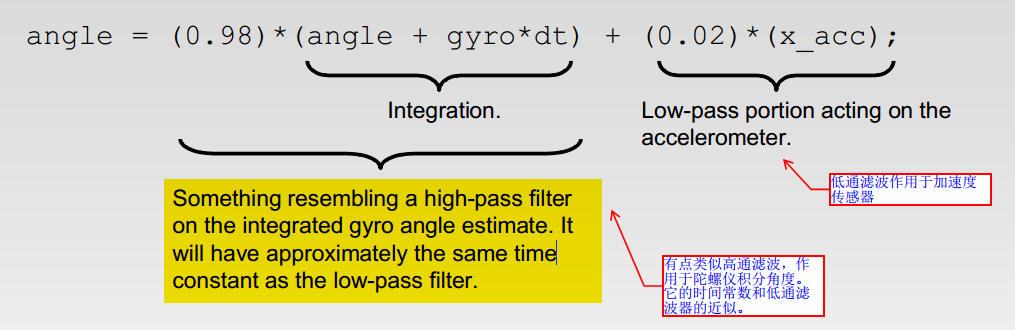
图1

看到这里，是不是觉得滤波其实也就那回事，并没有那么神秘高大上？滤波器的用途极广，只要你细心观察，滤波器的身影无处不在。

（二阶）互补滤波器

后来，互补滤波器经过不断演变发展，出现了二阶互补滤波器和滑动参数互补滤波器等变种滤波器。

附上二阶滤波代码供大家参考：

// newAngle 为加速度传感器经过atan2()转化后的角度值
// newRate 为陀螺仪角度值
// looptime 为计算周期
float Complementary2(float newAngle, float newRate, intlooptime)
{
float k = 10;
float dtc2 = float(looptime) / 1000.0;
x1 = (newAngle -   x_angle2C) * k * k;
    y1 = dtc2 * x1 + y1;
x2 = y1 + (newAngle -   x_angle2C) * 2 * k + newRate;
    x_angle2C = dtc2 * x2 + x_angle2C;
return x_angle2C;
}