数学建模
在上面简单分析中,通过类比倒立摆得到了小车直立的控制方案。下面对两轮自平衡小车进行简单数学建模,然后建立速度的比例微分负反馈控制,根据基本控制理论讨论小车通过闭环控制保持稳定的条件。
假设两轮自平衡小车简化成高度为L,质量为m的简单倒立摆,它放置在可以左右移动的车轮上。假设外力干扰引起小车产生角加速度 x(t)。沿着垂直于小车底盘方向进行受力分析,可以得到车体倾角与车轮运动加速度 a(t) 以及外力干扰加速度 x(t) 之间的运动方程。
 Image 3.3.1 - 小车运动方程 alt ><
Image 3.3.1 - 小车运动方程 alt ><
对应小车静止时,系统输入输出的传递函数为:
H(s)=(χ(s)Θ(s)=s2−Lg1)
此时系统具有两个极点:
sp=±√Lg
为了将上述计算结果可视化,我们可以根据传递函数
H(s)=(χ(s)Θ(s)=s2−Lg1)
,调用 Matlab 软件,绘制出传递函数的根轨迹示意图:
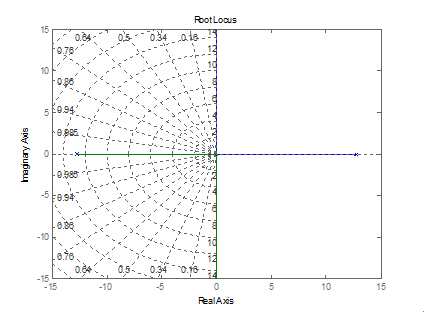
通过根轨迹示意图,可以很清晰的看出两轮自平衡小车的传递函数对应有两个零极点,有一个在 s 平面的右半平面。这说明两轮自平衡小车是不稳定的。
小车引入比例、微分(PD)反馈之后的系统如下图所示:
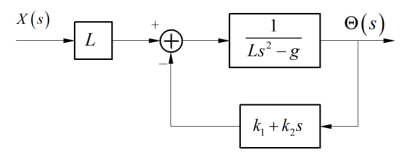 Image 3.3.2 - 加入比例微分反馈后的系统框图 alt ><
Image 3.3.2 - 加入比例微分反馈后的系统框图 alt ><
系统传递函数为:
H(s)=(χ(s)Θ(s)=s2+Lk2S+Lk1−g1)
此时两个系统极点位于:
sp=(2L−k2±√(K22−4l(K1−G)))
系统稳定需要两个极点都位于 s 平面的左半平面。要满足这一点,需要k1>g,k2>0。
为了将上述计算结果可视化,我们同样可以调用 Matlab 软件绘制当前系统传递函数的根轨迹图,并且求解极点值。
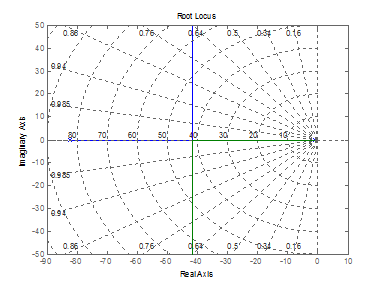 Image 3.3.3 - 两轮自平衡小车系统稳定时对应根轨迹极点 alt ><
Image 3.3.3 - 两轮自平衡小车系统稳定时对应根轨迹极点 alt ><
通过根轨迹图可以清晰地看出,此时系统传递函数的极点都已经分布在了 s 平面的左半平面,只要参数适合,极点的位置将会进一步远离 0 点,系统将会更稳定。
由此可以得出结论,当 k1>g,k2>0 时,两轮自平衡小车可以稳定。这与前面通过分析所得出的结论是一致的。



