PID控制原理与增量式PID算法
本小节纯粹在理论上讲解 PID 控制原理,先引出模拟 PID 控制公式,然后离散化处理,推导出位置式 PID 控制公式,再进一步推导出增量式 PID 控制公式。
将偏差的比例(Proportion)、积分(Integral)和微分(Differential)通过线性组合构成控制量,用这一控制量对被控对象进行控制,这样的控制器称 PID 控制器。
模拟 PID 控制
在模拟控制系统中,控制器最常用的控制规律是 PID 控制。为了说明控制器的工作原理,先看一个例子。下图所示是一个小功率直流电机的调速框图。
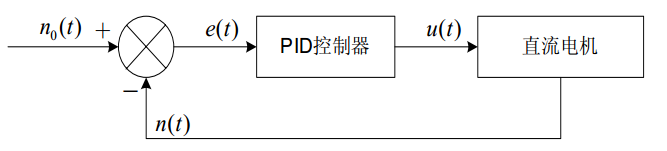 Image 5.14.1 - 小功率直流电机调速系统
Image 5.14.1 - 小功率直流电机调速系统
上图中,给定转速 n0(t) 与实际转速 n(t) 进行比较,其差值 e(t)=n0(t)−n(t),经过 PID 控制器调整后输出电压控制信号 u(t),u(t) 经过功率放大后,驱动直流电动机改变其转速。
抽象化的模拟 PID 控制系统原理框图,如下图所示。该系统由模拟 PID 控制器和被控对象组成。
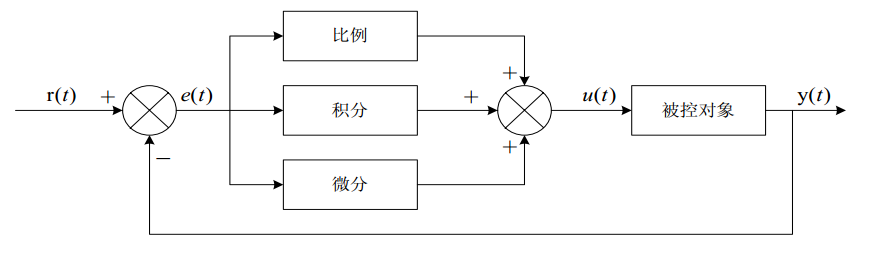 Image 5.14.2 - 模拟 PID 控制系统原理图
Image 5.14.2 - 模拟 PID 控制系统原理图
图中,r(t) 是给定值,y(t) 是系统的实际输出值,给定值与实际输出值构成控制偏差:
e(t)=r(t)−y(t) (式 1-1)
e(t) 作为 PID 控制的输入, 作为 PID 控制器的输出和被控对象的输入。 所以模拟 PID 控制器的
控制规律为
u(t)=kp[e(t)+Ti1∫e(t)dt+Tddtde(t)] (式 1-2)
其中,Kp 为控制器的比例系数,Ti 为控制器的积分时间,也称积分系数,Td为控制器的微分时间,也称微分系数。
数字 PID 控制
由于计算机的出现,计算机进入了控制领域。人们将模拟 PID 控制规律引入到计算机中来。对(式 1-2)的 PID 控制规律进行适当的变换,就可以用软件实现 PID 控制,即数字 PID 控制。
数字式 PID 控制算法可以分为位置式 PID 和增量式 PID 控制算法。
位置式 PID 算法
由于计算机控制是一种采样控制,它只能根据采样时刻的偏差计算控制量,而不能像模拟控制那样连续输出控制量,进行连续控制。由于这一特点,(式 1-2)中的积分项和微分项不能直接使用,必须进行离散化处理。离散化处理的方法为:以 T 作为采样周期,k 作为采样序号,则离散采样时间 kT对应着连续时间 t,用矩形法数值积分近似代替积分,用一阶后向差分近似代替微分,可作如下近似变换:
t≈kT(k=0,1,2,...)
∫e(t)dt≈T∑j=0ke(jT)=T∑j=0kej
dtde(t)≈Te(kT)−e[(k−1)T]=Tek−ek−1
上式中,为了表达的方便,将类似于 e(kT) 简化成 ek 等。
将(式 2-1)代入(式 1-2),就可以得到离散的 PID 表达式为
uk=Kp[ek+Ti(T)∑j=0kej+TdT(ek−ek−1)] (式 2-2)
或
uk=Kp∗ek+Ki∑j=0kej+KdT(ek−ek−1) (式 2-3)
其中,
k 为 采样序号,k = 0,1,2,...;
uk 为第 k 次采样时刻的计算机输出值;
ek 为第 k 次采样时刻输入的偏差值;
ek−1 为第 k-1 次采样时刻输入的偏差值;
Ki 为积分系数,Ki=kp∗TiT;
Kd 为微分系数,Kd=Kp∗TTd。
如果采样周期足够小,则 (式 2-2)或(式 2-3)的近似计算可以获得足够精确的结果,离散控制过程与连续过程十分接近。
(式 2-2)或(式 2-3) 表示的控制算法式直接按(式 1 -2) 所给出的 PID 控制规律定义进行计算的,所以它给出了全部控制量的大小,因此被称为全量式或位置式 PID 控制算法。
这种算法的缺点是:由于全量输出,所以每次输出均与过去状态有关,计算时要对 ek 进行累加,工作量大。并且,因为计算机输出的对应的是执行机构的实际位置,如果计算机出现故障,输出的将大幅度变化,会引起执行机构的大幅度变化,有可能因此造成严重的生产事故,这在实际生产际中是不允许的。
增量式 PID 算法
所谓增量式 PID 是指数字控制器的输出只是控制量的增量 △uk 。 当执行机构需要的控制量是增量,而不是位置量的绝对数值时,可以使用增量式 PID 控制算法进行控制。
增量式 PID 控制算法可以通过(式 2-2)推导出。由(式 2-2)可以得到控制器的第 k-1 个采样时刻的输出值为:
u(k−1)=Kp[e(k−1)+Ti(T)∑j=0k−1ej+TdT(e(k−1)−e(k−2))] (式 2-4)
用(式 2-2)减去(式 2-4)相减并整理,就可以得到增量式 PID 控制算法公式:
△uk=uk−uk−1=Kp[ek−ek−1+Ti(T)ek+TdTek−2ek−1+ek−2]
=Kp(1+TiT+TTd)ek−Kp(1+T2Td)ek−1+KpTTdek−2 (式 2-5)
=Aek+Bek−1+Cek−2
其中,
A=Kp(1+TiT+TTd);
B=Kp(1+T2Td);
C=KpTTd。
由(式 2-5)可以看出,如果计算机控制系统采用恒定的采样周期 T ,一旦确定 A、 B、 C,只要使用前后三次测量的偏差值,就可以由(式 2-5)求出控制量。
增量式 PID 控制算法与位置式 PID 算法(式 2-2)相比,计算量小的多,因此在实际中得到广泛的应用。
而位置式 PID 控制算法也可以通过增量式控制算法推出递推计算公式:
uk=uk−1+△uk (式 2-6)
(式 2-6)就是目前在计算机控制中广泛应用的数字递推 PID 控制算法。
采样周期的选择
香农(Shannon) 采样定律 :为不失真地复现信号的变化, 采样频率至少应大于或等于连续信号最高频率分量的二倍。根据采样定律可以确定采样周期的上限值。实际采样周期的选择还要受到多方面因素的影响,不同的系统采样周期应根据具体情况来选择。
采样周期的选择,通常按照过程特性与干扰大小适当来选取采样周期:即对于响应快、(如流量、压力) 波动大、易受干扰的过程,应选取较短的采样周期;反之,当过程响应慢(如温度、 成份)、滞后大时,可选取较长的采样周期。
采样周期的选取应与 PID 参数的整定进行综合考虑, 采样周期应远小于过程的扰动信号的周期,在执行器的响应速度比较慢时,过小的采样周期将失去意义,因此可适当选大一点;在计算机运算速度允许的条件下,采样周期短, 则控制品质好;当过程的纯滞后时间较长时, 一般选取采样周期为纯滞后时间的 1/4~1/8。

